Fénysebesség mérése¶
1. feladat: Ismerkedés a mérési elrendezéssel¶
Állítsa össze a mérési elrendezést! Ügyeljen arra, hogy a fényforrás és a detektor közti a fényút akadálymentes legyen. Az oszcilloszkópon folyamatosan mérve győződjön meg arról, hogy a detektált jel feszültsége ne haladja meg a 0,7 Voltot! Javaslat, a mérés során az oszcilloszkópon a 20 ns/osztás (kalibrált) időzítési állást használja, ezzel végrehajtható az összes mérési lépés.
Jellemezze az oszcilloszkópon mért jelalakokat egy tetszőlegesen választott tükörállás mellett!
Itt a helye a jellemzésnek
- jelalak kvalitatív jellemzése
- leolvasott jellemzői és a leolvasási hiba
Az 1-es csatornán mért jelalak egy négyszögjelre hasonlít, bár nem tökéletes. Egy rövid (kb. 30 ns-nyi) ideig nagyobb feszültséget kapunk, egyébként pedig a feszültség 0. A 2-es csatorna jele hasonló, bár a jel már sokban torzult. A lenti képen látható jelen például az első, nagyobb maximum jól látszik, de az impulzus többi része jobban eltűnt. Az ábra egy olyan elrendezés utáni állapotot mutat, amikor a fény az első távoli, azaz a 20 m-re lévő tükörről verődott vissza
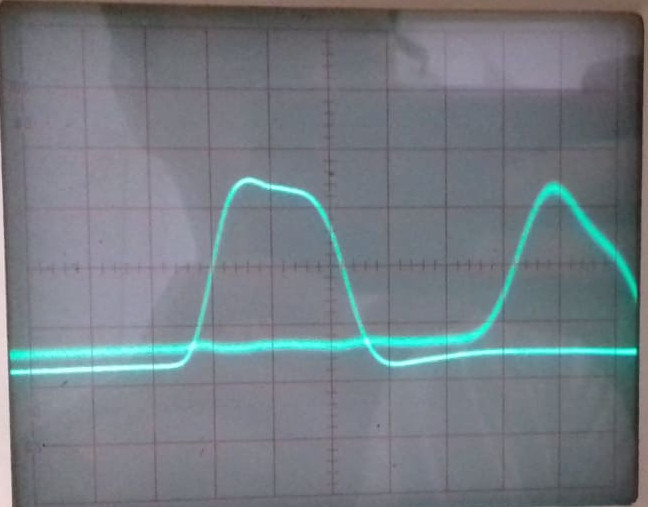
2. feladat: A fénysebesség mérése¶
Mérje meg az egyes tükörállásoknak megfelelő, az amplitúdó félmagasságában mért időkülönbségeket a jeladó és a jeldetektor jelei között! Mérje meg az időkülönbséget akkor is, ha a detektort egy rövid fényútnak megfelelő tükörpár köti össze az adóval. Az egyes tükörállásoknak megfelelő teljes fényút hosszokat, illetve a mért időkülönbségeket gyűjtse táblázatba. Megjegyzés: a laboratórium falain finom távolságjelzések találhatók, melyek segítik az optikai úthossz megállapítását.
Milyen hibák terhelik a mérési adatokat? Becsülje meg a mérési adatok hibáját!
Ábrázolja a mért adatokat és illesztés segítségével határozza meg a fénysebességet empirikus értékét, illetve az elektronika saját késleltetését!
| Mérési pont | fényút [m] | időkülönbség [ns] | időkülönsbség hibája [nm] |
|---|---|---|---|
| 1 | 1,01 | 42 | 2 |
| 2 | 20,26 | 104 | 2 |
| 3 | 27,28 | 126 | 4 |
| 4 | 33,74 | 144 | 8 |
| 5 | 52,20 | 206 | 10 |
A mért értékek a fenti táblázatban láthatók. Hibaforrás lehet a távolságmérés hibája és az oszcilloszkópról való leolvasás hibája.
Az első mérési pontot kivéve, a távolságokat nem én mértem, hanem csak leolvastam a falról, de feltételezzük, hogy akik mérték, 5 cm pontosságig meg tudták mérni a távolságokat. Ez még a legkisebb távolság esetében is 0,2%-os hibát jelent, ami mint látni fogjuk, elhanyagolható az időmérés hibájához, így ettől eltekinthetünk. (Az első mérési pont esetében az úthosszt én mértem le vonalzóval, ennek becsült hibája 1 cm, de ez is csak 0,99%-os hiba, amit szintén nem veszünk figyelembe)
Az időmérés hibája az oszcilloszkóp leolvasási hibája. Mivel a ábrázolt jelnek van vastagsága, nem lehet pontosan megállapítani, hogy hol metszi a középső tengelyt, így ez a legjobb esetben is okoz egy fél beosztásnyi hibát. (Mivel 5 beosztás 20 nm, ezért a fél beosztásnyi hiba 2 ns-nak felel meg.) Amikor a fény már nagyobb távolságokat tesz meg, akkor az érzékelt intenzitás csökken, így a mért jel is kisebb, így az oszcilloszkóp érzékenységét erősebbre kellett állítani, ezáltal a vonal még vastagabb lett, és a leolvasás pontossága rosszabb lett, ezért a nagyobb távolságok esetén nagyobb a hiba.
%pylab inline
from scipy.optimize import curve_fit
# adatrögzítés, ábrázolás és illesztés
def linear(x, a0, a1):
return x*a1 + a0
# Az oszlopok jelentése: fényút, fényút hibája, időkülönbség, időkülönbség hibája
adatok_tukor = array([[ 1.01, 0.01, 42, 2 ],
[ 20.26, 0.05, 104, 2],
[ 27.28, 0.05, 126, 4],
[ 33.74, 0.05, 144, 8],
[ 52.20, 0.05, 206, 10]])
eh, hiba_tukor = curve_fit(linear, adatok_tukor[:, 0], adatok_tukor[:, 2], sigma=adatok_tukor[:, 3])
figsize(12, 8)
errorbar(adatok_tukor[:, 0], adatok_tukor[:, 2], yerr=adatok_tukor[:, 3], marker="x", markeredgecolor="red", markersize=10, ecolor="red", linestyle="None", label="mért adatok")
x = linspace(adatok_tukor[:, 0][0], adatok_tukor[:, 0][-1], 100)
plot( x, eh[0] + eh[1] * x, "c-", lw=0.7, label="illesztett egyenes")
xlabel("fényút [m]", size=15)
ylabel("időkülönbség [ns]", size=15)
title("Az időkülönbség a fényút függvényében", size=21, y=1.03)
legend(fontsize="large")
print("együtthatók:", eh)
print("hibamátrix:", hiba_tukor)
A becsült fénysebesség hibával: ( 3,13 $\pm$ 0,02 ) *10^8 m/s.
Az elektronika becsült késleltetése: 38,6 $\pm$ 0,4 ns.
3. feladat: Az üvegszál vizsgálata¶
**Figyelem:** a feladatban használt optikai szál nagyon régi, a korábbi évek során elszenvedett mechanikai hatásokat megszenvedte, így a tovaterjedő jel nehezen mérhető rajta, sok türelmet igényel! Javaslat, hogy ezt a feladatot csak a labor végén végezze el!
Mérje meg a fényvezető kábelen a jel terjedési idejét, és ez alapján becsülje meg az üvegszálnak a törésmutatóját!
A kábel hossza 20,06 m.
A mért jelterjedési idő 138 $\pm$ 10 ns.
Ez alapján a fényvezető szál becsült törésmutatója adja meg a képletet is!
A mérési adatok alapján a fény terjedési sebessége az üvegkábelben: $c_{üveg} = \frac{l_{kábel}}{t_{terjedés}} = \left( 1,5 \pm 0,1 \right) 10^8\,\frac{m}{s}$
Amiből már adódik a törésmutató: $n = \frac{c_{vákuum}}{c_{üveg}} = 2,1 \pm 0,2$
4. feladat: Jelterjedés vizsgálata koaxiális kábelben¶
Mérje meg az elektronikus jelek terjedési sebességét a koaxiális kábelen!
A kábel hossza 19,2 m
A mért propagációs idő 96 $\pm$ 2 ns.
Ez alapján a jelek terjedési sebessége a koaxiális kábelen (2,00 $\pm$ 0,04) * 10^8 m/s, ami a fény vákuumbeli segességének körülbelül 0,64 $\pm$ 0,02 szorosa.
Visszaverődések vizsgálata koaxiális kábelben¶
Ha a koaxiális kábel csatlakozási pontjai nincsenek helyesen lezárva, akkor a rajta átvezetett jel formája torzul a visszaverődések miatt. Mérje meg a vezeték bemenő oldalán a gerjesztés amplitudójának valamint a visszavert jel amlitudojának nagyságának arányát különböző lezáró ellenállásérték megválasztása mellett! Ehhez kapcsolja a koaxiális kábel végére a mérőhelyen elhelyezett ellenállássort.
A lezáró ellenállás aktuális értékét úgy állíthatja be, hogy az ellenállások mellett található söntölő kapcsolókat (jumperek) lehúzza. Így a lehetséges ellenálláskombinációk széles skáláját elő tudja állítani.
Az adatokból illesztés segítségével állapítsa meg a kábel hullámellenállását és a veszteségi tényezőt! Javaslat: az adatok ábrázolásánál érdemes a vízszintes tengelyt logaritmikusra választani. Ábrázolja az adatokat és illesszen rájuk egy alkalmas fügvényt.
| Mérés száma | Lezáró ellenállás [ $\Omega$ ] | Amplitúdóarány | Amplitúdóarány hibája |
|---|---|---|---|
| 1 | 10 | -0,533 | 0.02 |
| 2 | 33 | -0,135 | 0.02 |
| 3 | 43 | -0,081 | 0.01 |
| 4 | 51 | 0,041 | 0.01 |
| 5 | 61 | 0,108 | 0.01 |
| 6 | 84 | 0,230 | 0.02 |
| 7 | 220 | 0,514 | 0.02 |
# adatrögzítés, ábrázolás és illesztés
def koaxos(x, q, r0):
return q * (x - r0) / (x + r0)
# oszlopok jelentése: lezáró ellenállás, amplitúdóarány, amplitúdóarány hibája
adatok_koax = array([[ 10, -0.53, 0.02 ],
[ 33, -0.14, 0.02],
[ 43, -0.08, 0.01],
[ 51, 0.04, 0.01],
[ 61, 0.11, 0.01],
[ 84, 0.23, 0.02],
[ 220, 0.51, 0.02]])
(q, r0), hiba_koax = curve_fit(koaxos, adatok_koax[:, 0], adatok_koax[:, 1], sigma=adatok_koax[:, 2])
figsize(12, 8)
errorbar(adatok_koax[:, 0], adatok_koax[:, 1], yerr=adatok_koax[:, 2], marker="x", markeredgecolor="red", markersize=10, ecolor="red", linestyle="None", label="mért adatok")
x = linspace(adatok_koax[:, 0][0], adatok_koax[:, 0][-1], 100)
plot(x, koaxos(x, q, r0), label="illesztett görbe")
semilogx()
xlabel(r"Lezáró ellenállás $[\Omega]$", size=15)
ylabel(r"Amplitudóarány", size=15)
title("Az amplitudóarány a lezáróellenállás függvényében", size=21, y=1.03)
legend(fontsize="large")
print("Paraméterek: q:", q, "r0:", r0)
print("hibamátrix:", hiba_koax)
Az illesztésnél használt modellfüggvény egyenlete $ \frac{U_{vissza}}{U_{be}} = Q \frac{R - R_0}{R + R0} $, amely alapján a hullámellenállás 48 $\pm$ 1 $\Omega$ és a veszteségi tényező 0,82 $\pm$ 0,04 adódik.
A méréssel kapcsolatos észrevételek¶
Kitölteni nem kötelező:
- Itt kérjük feltűntetni, hogy mennyi idő volt szükséges a feladatok elvégzéséhez.
- Itt lehet javaslatot tenni a méréssel kapcsolatban.
- A méréssel kapcsolatban felmerült további ötletek.
Abszolút korrekt mérés, nem kell agyon szöszölni az egészet, de azért nem is túl könnyű, annyit kell dolgozni hozzá, amennyi szerintem elvárható (és eltűrhető) egy labormérésen. A téma is érdekes, legalább is én szeretem, ha nem valami random dolgot kell kimérni, hanem valami szemléletes mennyiséget (pl. adott esetben a fénysebességet). Magát a mérést kb. 2 óra alatt végeztem el úgy, hogy elég ráérősen csináltam, és közben nem jött be semmi komplikáció. A jegyzőkönyvvel együtt bőven megcsinálható a 3,5 órás időmennyiség alatt (talán még ebédelni is lenne idő), én is csupán a ráérősségem miatt nyúltam túl.
Imponatív kezdés volt, ha a tárgy többi mérése is ilyen lesz, az határozottam pozitív.